Nasycená hydraulická vodivost - dvouválcový infiltrometr

Nasycená hydraulická vodivost je jednou z nejdůležitějších hydrofyzikálních charakteristik. Její stanovení se vyžaduje pro mnoho různých aplikací, neboť je klíčovým parametrem pro řešení úloh v hydropedologii, hydrogeologii, ochraně životního prostředí - zejména pak ochraně půdy a podzemní vody před znečištěním, rekultivaci půd, závlahy a odvodnění pro účely zemědělské i nezemědělské, jako např. skládková hospodářství, sportovních povrchů apod. Je to také jeden z hlavních datových vstupů pro simulační modelování transportu vody a roztoků půdním profilem. Zatřídění zemin podle nasycené hydraulické vodivosti se provádí podle Tab 1.

Tab 1. Tabulka pro zatřídění zemin podle nasycené hydraulické vodivosti - převzato z již neplatné normy ČSN 721020 Laboratorní stanovení propustnosti zemin. V současnosti platná norma ČSN 17892 Geotechnický průzkum a zkoušení – Laboratorní zkoušky zemin, Část 11: Stanovení propustnosti zemin při konstantním a proměnném spádu již uvedenou tabulku neobsahuje.

Zemina (podle relativní propustnosti ČSN 73 68 50)	Přibližné rozmezí nasycené hydraulické vodivosti K (m s-1)	Třída zeminy podle ČSN 73 10 01	Příklady druhů zemin
velmi nepropustná	< 10-10	F6 F7 F8	Jíly s nízkou a střední plasticitou Jíly a hlíny s vysokou až extrémně vysokou plasticitou
nepropustná	10-8 až 10-10	F1 F2 F4 F5	Hlíny štěrkovité Jíly štěrkovité a písčité Hlíny s nízkou a střední plasticitou
málo propustná	10-6 až 10-8	F3 S3 S5 G4 G5	Hlíny písčité Písky hlinité a jílovité Štěrky hlinité a jílovité
propustná	10-4 až 10-6	S3 G3	Písky a štěrky s příměsí jemnozrnné zeminy (5 – 15 %)
velmi propustná	> 10-4	S1 G1 S2 G2	Písky a štěrky dobře a špatně zrněné, tj. čisté písky a štěrky, písčité štěrky, písky a štěrky s velmi malou příměsí jemnozrnných zemin (<5%)

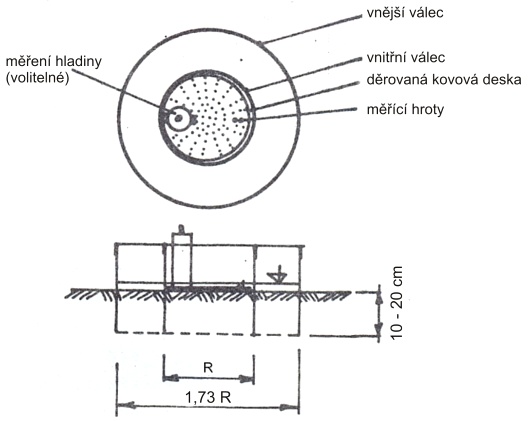
Dvouválcový infiltrometr (Parr and Bertrand, 1960) Jedná se o dnes již klasickou metodu infiltračních testů, používanou pro celou řadu aplikací, např. pro návrh rozchodů systematické trubní drenáže, návrh sportovních hřišť, golfových ploch, izolačních vrstev skládek komunálního odpadu apod. Infiltrometr se skládá ze dvou soustředných válců (viz Obr 1), které jsou zaraženy do země, a děrované vnitřní desky s měřícími hroty. Pomůcky Dvouválcový infiltrometr, dřevěný trámek nebo jiná vhodná pomůcka pro zarážení válců, kladivo vhodné velikosti, plastový kbelík, odměrná nádoba, nůžky na vegetaci, nůž, stopky, psací potřeby a formulář pro zápis dat, skládací metr, hadr, dostatečné množství vody.

Obr 1. Schéma dvouválcového infiltrometru.

Postup při terénním experimentu

Měření se provádí ve vnitřním válci, vnější válec má za úkol jen zachovávat svislost proudnic pod válcem vnitřním při infiltraci. Uvnitř vnitřního válce je umístěna děrovaná kruhová deska se dvěma hroty, které slouží k odečítání poklesu hladiny. Deska také zabraňuje rozplavení zeminy při doplňování vody pro infiltraci (viz Obr 1).


Válec se zarazí do hloubky cca 10 - 20 cm pod terén (je vhodné nejprve po obvodu válců rozříznout travní drn nožem, půda se tak méně rozruší), umístí se kruhová deska s hroty a do obou válců současně se nalije voda tak, aby ve vnitřním dosahovala na vyšší hrot. V té chvíli se spustí stopky a měří se čas, za který poklesne hladina z úrovně horního hrotu na úroveň hrotu dolního.


Za tuto dobu zasákne určité množství vody (v našem případě 500 ml). Ve chvíli dosažení dolního hrotu se odečte čas a dolije opět stejné množství vody z odměrné nádoby (500 ml). Ve vnějším válci se hladina udržuje na úrovni vnitřního válce. Metoda je vhodná spíše pro orientační stanovení, které však v řadě případů zcela postačuje.

Zápis dat a výpočty z terénního experimentu

Změřená data zaznamenáváme do připraveného formuláře jako je např. zde vpravo. Formulář zahrnuje také nezbytné parametry pro tento konkrétní dvouválcový infiltrometr, který je demonstrován na fotografiích a videích. Tyto parametry se pro jiné dvouválcové infiltrometry mohou lišit! Změřená data i(t) se vynesou do grafu pro vizuální kontrolu naměřených dat (mm papír v terénu nebo MS Excel). Změřená data se vyhodnotí za použití Philipových rovnic infiltrace (Philip, 1957):

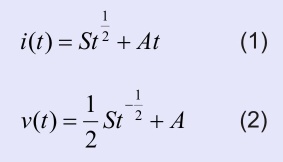kde i(t) je kumulativní infiltrace, S je sorptivita, t je čas a A je parametr

Měření poskytlo hodnoty i a t v rovnici (1) zbývá nalézt dva parametry S a A optimálně tak, aby křivka, popsaná rovnicí (1) co nejtěsněji procházela změřenými body. Pro tento účel se používá známé metody minima čtverců. Po získání uvedených parametrů S a A se hodnoty rychlosti infiltrace v v libovolném čase vypočtou ze druhé Philipovy rovnice (2).
Vyrovnaná rychlost infiltrace po delším čase infiltrace (křivka rychlosti je rovnoběžná s osou vodorovnou, tedy času t) je svou hodnotou konstantní a blíží se nasycené hydraulické vodivosti K. Přibližně platí, že:

kde K je nasycená hydraulická vodivost a m je konstanta o hodnotě 0,66667 (= 2/3)

Vypočtená hodnota K se může zatřídit podle Tab 1.

Příklad analýzy dat

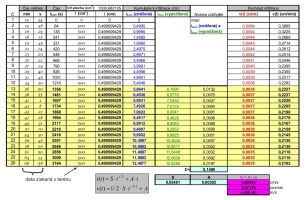
Viz tabulka vpravo. Změřená data se upraví, kumulativní infiltrace v objemových jednotkách se pomocí infiltrační plochy přepočítá na výšku zainfiltrované vody v délkových jednotkách. Kumulativní infiltraci v čase vyneseme do grafu a na křivce určíme lineární část, kdy už je rychlost infiltrace vyrovnaná (žlutá část tabulky). Z této lineární části pak spočítáme parametry S a A z rovnice (1) metodou minima čtverců. Využijeme funkci ŘEŠITEL v MS Excel. (Řešitele najdeme v Nástrojích, pokud ne, tak ho aktivujeme v Doplňcích.) Hledáme takovou přímku, která bude prokládat přímkovou část našich změřených dat a bude se od ní co nejméně lišit, tzn. součet druhých mocnin odchylek obou přímek musí být co nejmenší.

Do sloupce i_kumvypočítaná vložíme vzorec (rovnice 1). Do vzorce vložíme absolutní odkazy na buňky s hledanými parametry S a A, do kterých vložíme libovolné počáteční hodnoty, např. 0,5 (světle modré buňky). Do dalšího sloupce vložíme druhou mocninu rozdílu kumulativní infiltrace změřené a vypočítané, a také sumu těchto hodnot, jak je zobrazeno v tabulce. Tuto buňku se sumou hodnot nastavíme v Řešiteli, že má být minimální. Jako měněné buňky označíme ty, ve kterých máme počáteční hodnoty parametrů S a A a potom spustíme řešení. Při dodržení správného postupu budou nalezeny parametry S a A funkce optimálně tak, aby byla změřená data dobře proložena, což ověříme na grafu (viz Obr 2). Zjištěné parametry pak použijeme i k výpočtu vyrovnané rychlosti infiltrace a nasycené hydraulické vodivosti K.


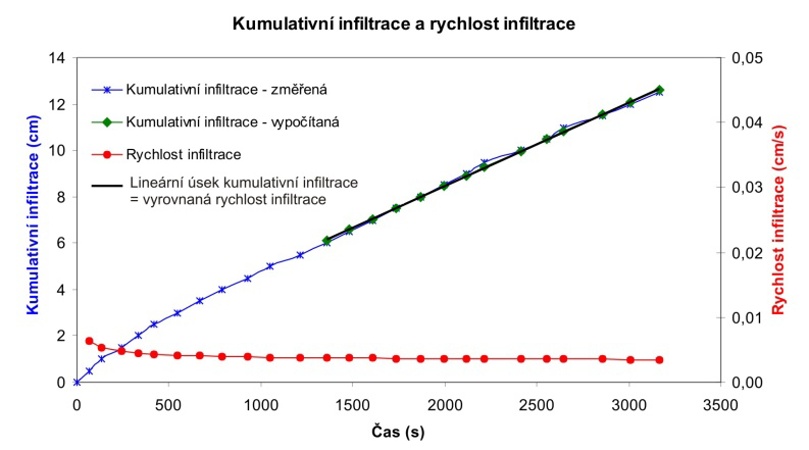
Obr 2. Kumulativní infiltrace a rychlost infiltrace.

Literatura

ČSN 721020 Laboratorní stanovení propustnosti zemin

ČSN 17892 Geotechnický průzkum a zkoušení – Laboratorní zkoušky zemin, Část 11: Stanovení propustnosti zemin při konstantním a proměnném spádu

Matula, S., and C. Dirksen. 1989. Automated regulating and recording system for cylinder infiltrometer. Soil Science Society of America Journal 53:299-302.

Parr, J.R., and Bertrand, A.R. (1960) Water infiltration into soils. Advances in Agronomy, 12, 311-363.

Philip, J.R. (1957) The theory of infiltration: 4. Sorptivity and algebraic infiltration equations Soil Science 84, 257-264.