Saturated hydraulic conductivity: Pressure infiltrometer

Pressure infiltrometer (Matula and Kozáková, 1997)

This relatively simple pressure infiltrometer is a Mariotte type infiltrometer constructed from non-corrosive materials (Plexiglas, PVC, Teflon). The device uses the mechanical-hydraulic principle without need of an external energy supply. The device is portable and easy to set up and can be operated by one or two workers. The device enables the measurement with acceptable accuracy of the cumulative infiltration of ponded water from the infiltration ring. The metal infiltration ring (inner diameter of 15 cm) is equipped by its own water gauge for reading the constant water level H in the infiltration ring at a certain time after the start of the infiltration experiment. The depth of metal ring penetration into the soil can be up to 10 cm.
The infiltrometer can supply water during the experiment up to the amount corresponding with saturated hydraulic conductivity
K=77 m day^-1.


Watch the video in order to see how to use this pressure infiltrometer.

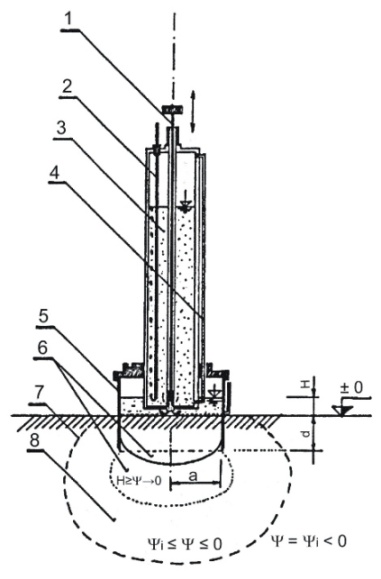Description of the infiltrometer 1 - Piston valve to open or close the water outlet 2 - Moveable air tube to set the applied water pressure H on infiltrating surface 3 - Marriote type water reservoir 4 - Plexiglass tube of a small diameter to enable accurate fading of the water level 5 - Iron ring with a radius of a driven into the soil to the depth d 6 - Bulb of field saturated soil 7 - Wetting front 8 - Wetted zone Tab 1. The important details about the infiltrometer are summarised in the following table.

Fig 1. Schema of the Pressure infiltrometer (Matula and Kozáková, 1997).

Measurement procedure

The selected spot for the infiltration experiment needs to be prepared first; the grass needs to be cut (or removed). It is also possible to apply this device on the stages of the soil pits. The infiltration ring is then driven (hammered, but with minimum disturbance to the soil) into the soil to the position of the water gauge. A protective pad from the porous material is placed into the infiltration ring to protect the soil surface against clogging. The infiltrometer is then placed on the infiltration ring; the water reservoir is filled with water from a portable water reservoir. Before taking the device into the field, the level of ponded water in the ring was pre-set on the infiltrometer in the laboratory (i.e. 10 cm).

When the valve at the top infiltrometer is opened, the infiltration experiment starts. After several seconds the soil surface inside the infiltration ring is ponded with water, the water level in the infiltration ring rises until it reaches its constant value. The water level in the infiltration ring can be monitored in the water gauge. From the start of the experiment, the time is being measured, and the time needed for constant water level formation in the infiltration ring is recorded. Drops in the level of water in the water reservoir are recorded at selected time intervals (eg. 2 minutes). A data record form for the pressure infiltrometer (Matula and Kozáková, 1997) is on the right.

It is important to determine the initial conditions (initial water content in the soil) of the soil before the infiltration starts. The initial soil water content can be determined gravimetrically from disturbed soil samples taken by the soil sampler close to the infiltration ring or in-situ by using one of the indirect methods (TDR, FDR, capacitance…). The outcome of the infiltration tests are the cumulative infiltration data I (expressed as water level drops in cm – recalculation to the volume of infiltrated water per area of the infiltration surface is needed!!! Infiltration area of the infiltration ring needs to be considered for calculation of actual infiltration rate, too!) with time Δt (min) in the particular selected time intervals (see the prepared form for the data record above). The infiltration test should last until the steady-state infiltration rate is reached; that means the same volume of water is infiltrated for several consecutive time intervals.

Theory behind the data analysis and example of data analysis

The steady-state infiltration, which takes place after longer time period of water infiltration, is generally described by an equation from Reynolds and Elrick (1991) and Reynolds et al. (1985) which has the following form:

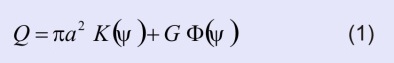where Q is the amount of infiltrated water (L3 T-1), a is the radius of the infiltration ring (L), G is the function of the infiltration surface geometry (L), Φ is the flow potential (L2 T-1), ψ is the water potential (expressed as pressure head h in length units (L).

Equation (1) for the pressure infiltrometer is further transformed into the following form (Elrick and Reynolds, 1992):

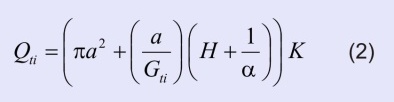where Qti is the steady infiltration (L3 T-1), a is the radius of the infiltration ring (L), Gti is the shape factor (L3 T-1), H is the hydraulic head of ponded water in the infiltration ring (L), α is a parameter (L-1) (Philip, 1985 and 1987; for pressure infiltrometers details can be found in Elrick and Reynolds, 1989), K is the saturated hydraulic conductivity (L T-1).

where d is the penetration depth of the infiltration ring into the soil (L) and a is the radius of the infiltration ring (L)

Based on equation (2) and other equations (details in Elrick and Reynolds, 1989), the following equation for saturated hydraulic conductivity K was formulated:


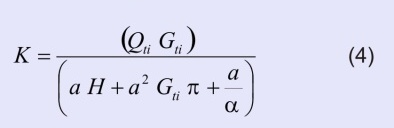
The above equation (4) can be used for pressure infiltrometer data analysis (see Tab 2), where parameter α = 12 m^-1 (= most structured soils and medium and fine sands) and Q_ti (cm³ min^-1) can be calculated as follows (eq. 5).

where h is the water level drop in the infiltrometer reservoir after the elapsed time interval Δt

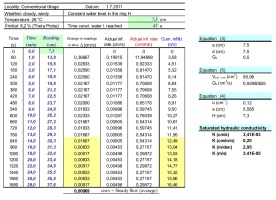
Tab 2. Example of saturated hydraulic conductivity calculation.

In equation (5) only steady-state infiltration data, obtained after longer time of infiltration, can be used (the yellow part in table Tab 2). It can be useful to plot the Q_ti as a function of time t into a graph and find the best possible fit of the measured points by a straight line, see Fig 2.


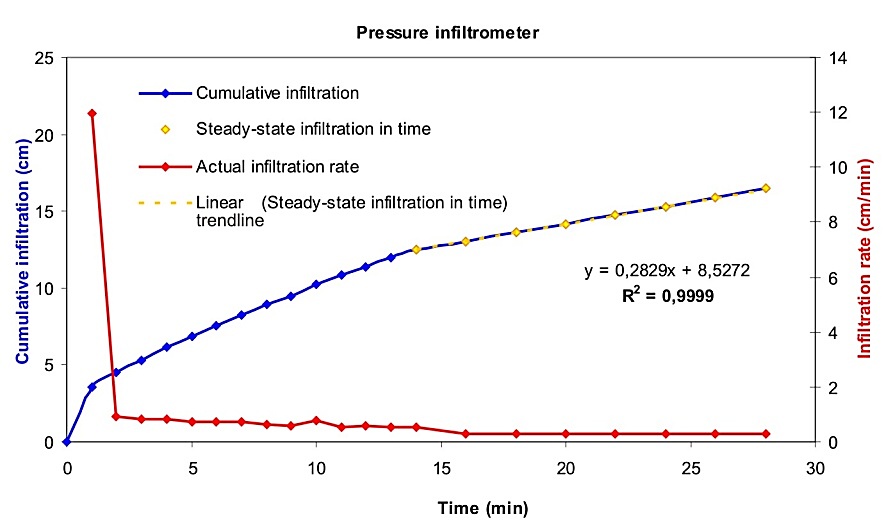
Fig 2. Cumulative infiltration and infiltration rate.

The calculated value of K is then used for soil classification according to the Soil classification table which can be found on the Double ring infiltrometer page (Tab. 1.)

References

Elrick, D.E., and Reynolds, W.D. (1989) Water Flux Components and their measurements. Proc. App. Soil Physics in Stress Environments. Jan 22-26 NARC. Islamabad, Pakistan.

Elrick, D.E., Reynolds, W.D. (1992) Methods for analysing constant head well permeameter data. Soil Science Society of America Journal, 56, 309-312.

Matula, S., Kozáková, H. (1997) A simple pressure infiltrometer for determination of soil hydraulic properties by in situ infiltration measurements. Rostlinná výroba, 43, 405-413.

Reynolds, W.D., Elrick, D.E. (1991) Determination of hydraulic conductivity using a tension infiltrometer. Soil Science Society of America Journal, 55, 633-639.

Reynolds, W.D., Elrick, D.E., Clothier, B.E. (1985) The constant head well permeameter: effect of unsaturated flow. Soil Science, 139, 172-180.

Philip, J.R. (1985) Approximate analysis of the borehole permeameter in unsaturated soils. Water Resources Research, 21, 1025-1033.

Philip, J.R. (1987) The quasilinear analysis, the scattering analog, and other aspects of infiltration and seepage. In: Y.S. Fok (Ed.) Infiltration, development and application. Water resources Research Center, Honolulu, USA, 1-27.